Hi Everyone, My post today is about Data Compression Techniques, I’ve decided to post about Data Compression because It’s really widely used everywhere around us in many applications that we are using everyday… I really like this CS topic trying everyday to know more about it… Today I’ll be talking about:
First, Simply There is 2 main techniques in data compression:
2. Lossy Compression: Because sometimes we need to save size and time we are using this technique; Lossy Compression is not accurate 100%, This Compression technique is used in analog ranged data such as videos, JPEG encoding and sounds. and now let’s talk about the most known fast Lossless Data Compression Algorithms that are used nowadays: Huffman and Lempel-ZIV coding … let’s take a look on them Examples of Lossless Data Compression Algorithms1-Huffman Algorithm:A Huffman code is designed by merging together the two least probable characters, and repeating this process until there is only one character remaining. A code tree is thus generated and the Huffman code is obtained from the labeling of the code tree. An example of how this is done is shown below.  The final static code tree is given below:  2-Lempel-Ziv Coding (LZ Coding): The basic idea is to parse the input sequence into non-overlapping blocks of different lengths while constructing a dictionary of blocks seen thus far. Encoding Algorithm:
Example of Lossy Data Compression Algorithms1-Discrete Cosine Transform (DCT) Algorithm:expresses a finite sequence of data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio (e.g. MP3) and images (e.g. JPEG) (where small high-frequency components can be discarded) (Wikipedia) you can take a look on this Demo Java Applet that applies the DCT Algorithm: http://www.comp.nus.edu.sg/~cs5248/0910S2/l01/DCTdemo.html DCT Simulation tool: http://pi4.informatik.uni-mannheim.de/pi4.data/content/animations/dct_2d/index.html e.g. Consider this 8x8 grayscale image of capital letter A. 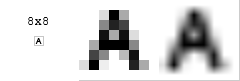 Original size, scaled 10x (nearest neighbor), scaled 10x (bilinear). DCT of the image.   Basis functions of the discrete cosine transformation with corresponding coefficients (specific for our image). Each basis function is multiplied by its coefficient and then this product is added to the final image.  On the left is final image. In the middle is weighted function (multiplied by coefficient) which is added to the final image. On the right is the current function and corresponding coefficient. Images are scaled (using bilinear interpolation) by factor 10x. you can know more about DCT here : https://www.tach.ula.ve/vermig/DCT_TR802.pdf [1] Compression Ratio: It’s the ration between the bits of data before compression and the Bits of data after compression ( Original Bits:Compressed Bits) e.g. if we have a file with an original data size of 65,535 bytes .. This file became 16,384 bytes after applying some data compression algorithms on it. we can say that the compression ratio is 65535:16384 which is approximately 4:1 or we can just say now that the file is 75% compressed (The total size is 100% and the compressed size is 25% of the total); Now if we have 8 bits per each byte we can say that we are representing each byte by just 2 bits (25 %) or 2 bits per byte or 2 bits/character *The Difference between the Original data and the Reconstruction data is called “Distortion” also “Fidelity” and “Quality”.
[2] The entropy rate of a source: is a number which depends only on the statistical nature of the source. If the source has a simple model, then this number can be easily calculated. Here, we consider an arbitrary source:
Zero-Order Model: The characters are statistically independent of each other and every letter of the alphabet, For English text, the alphabet size is m=27. Thus, if this had been an accurate model for English text, then the entropy rate would have been H=log2 27=4.75 bits/character. References: 2-A. Gersho and R. M. Gray, Vector Quantization and Signal Compression. 3-D. A. Huffman, ``A Method for the Construction of Minimum Redundancy Codes,'' Proceedings of the IRE, Vol. 40, pp. 1098--1101, 1952. 4-J. Ziv and A. Lempel, ``A Universal Algorithm for Sequential Data Compression,'' IEEE Transactions on Information Theory, Vol. 23, pp. 337--342, 1977. 5-J. Ziv and A. Lempel, ``Compression of Individual Sequences Via Variable-Rate Coding,'' IEEE Transactions on Information Theory, Vol. 24, pp. 530--536, 1978. 6-T. A. Welch, ``A Technique for High-Performance Data Compression,'' Computer, pp. 8--18, 1984. 7.C. E. Shannon, ``Prediction and Entropy of Printed English," available in Shannon: Collected Papers. Hope you enjoyed this Data Compression Introduction and Thanks for Reading; | ||
| For More Info Please Visit Data Compression - Debra A. Lelewer and Daniel S. Hirschberg |
Thursday, August 22, 2013
Data Compression Techniques - 1
Subscribe to:
Comments (Atom)
AI-Enabled Risk Scoring for TPPs in Open Banking: A Game Changer for Ecosystem Trust
As Open Banking ecosystems mature globally, traditional banks, fintech startups, and regulators face a growing challenge: how to trust the g...
-
Hi Everyone, My post today is about Data Compression Techniques, I’ve decided to post about Data Compression because It’s ...
-
This Post has some Previous Posts, you can access the first Main Post here: Some C++ Problems for Beginners (1) The code ...

